一文详解AMC数学竞赛！涵盖AMC8/10/12~

　　AMC(英文全称：American Mathematical Competition)是美国数学协会(MAA，Mathematics Association of America)举办的一系列美国数学竞赛，包括AMC8、AMC10、AMC12、AIME、USJMO、USAMO。AMC竞赛自1950年举办以来，已经成为全球范围内极具影响力的数学竞赛之一。AMC竞赛不仅检验学生的数学知识，更重要的是培养学生的逻辑思维。除此之外，无论是在申请国内重点初中的自主招生(例如上海三公)，申请过外出名校，AMC成绩都是名校申请加分项。

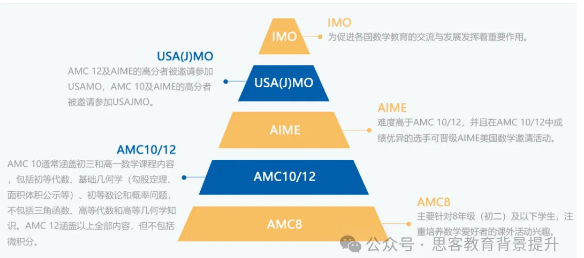
　　哪些学生适合参加AMC数学竞赛?

　　AMC美国数学竞赛分为三个不同的等级，分别是AMC8，AMC 10，AMC12，学生可根据自己的年龄及年级情况，来选择参加相应的级别考试。

　　那些在AMC12和AMC10中成绩优异的学生，将被邀请参加AIME美国数学邀请赛。这是选拔参加美国数学国家队和美国数学奥林匹克USAMO的竞赛的选拔赛。

　　AMC8/10/12竞赛规划

　　AMC8竞赛规划思路：

　　小学的学生提前学习，培养数学思维，提升英语能力，对孩子们来说，可以先准备AMC8。

　　可以通过AMC8竞赛，一方面培养数学思维，同时把英语也练习起来。但是参加AMC8竞赛的大多是为了小升初以及为了AMC10和AMC12打基础的。

　　对于3-8年级，尤其3-6年级的小学生，AMC竞赛性价比很高的原因:

　　①与体制内小学奥数相比，考察广而不深，更适合不同基础的学生参加;

　　②体制内禁赛，国际竞赛成为新选择，学生可通过AMC竞赛证明自己的数学能力;

　　③低龄竞赛天花板，高含金量，小升初/国际学校认可;

　　AMC10竞赛规划思路：

　　AMC10竞赛接轨真实竞赛水平，初高中学生新挑战，在提升思维的同时，为更高阶竞赛做好充分准备。

　　基础一般的学生，8、9年级开始准备，基础相对比较好的同学，可以在6/7年级的时候开始准备。

　　AMC12竞赛规划思路：

　　AMC12海外名校高度认可，部分名校官网会要求学生填写AMC或AIME竞赛成绩，提升学生入学竞争力。

　　基础一般的学生，10年级开始准备，提前打基础，基础较好的学生，可以9年级开始准备。

　　AMC8/10/12考试内容

　　AMC8数学竞赛考察内容

　　AMC8数学竞赛考察内容主要由三个部分组成，小学校内知识，小学奥数知识，和初中校内知识，

　　AMC8竞赛考试范围包括了组合、几何、代数、数论这四大类。

　　AMC10竞赛知识点汇总

　　01立体几何

　　点线圆的关系、三维坐标系、立体几何作图、正多面体，欧拉公式、特殊的立体几何图形、立体几何技巧

　　02进阶几何

　　进阶几何作图、三角形进阶、正弦定理、余弦定理、内切圆和外切圆、斯图瓦尔特定理、共点和共线、圆和四边形、四点共圆、圆的外切四边形、正多边形、角度、周长和面积、进阶平面几何技巧、解析几何入门

　　03进阶组合

　　容斥原理、二项式定理及相关结论、进阶排列、组合和概率

　　期望入门、递推、二分法、进阶组合方法

　　04进阶代数

　　多项式、余数定理、韦达定理、根与系数的关系、特殊高次方程、进阶不等式、均值不等式、函数入门、定义域和值域、二次函数、指数函数、对数函数、简单三角函数、数列进阶、代数技巧进阶

　　05进阶数论

　　数，数组和序列、模运算，复杂同余问题、整数、分数和小数，进制转换、基本丢番图方程、进阶数论技巧

　　AMC12竞赛知识点汇总

　　以代数、几何、数论、组合四个模块的知识为主，但核心知识层面上多出了对数、三角函数的计算与图像、复数三个知识模块的考察，并且这三个模块在AMC12中几乎100%会出题考察。

　　往年知识模块占比供参考

　　进阶代数

　　复杂不等式、调和不等式、轮换不等式、柯西不等式;复杂函数问题，反函数和符合函数，三角函数和差化积、积化和差，万能公式;复数，复平面，欧拉公式，蒂莫夫公式;数学归纳法、复杂数列和极限

　　进阶几何

　　圆相关几何进阶;数形结合，二维、三维图形的函数表达，进阶解析几何;不规则二维、三维图形的处理;二维向量、三维向量

　　进阶数论

　　二次余数，高次余数、费马圣诞节定理、费马小定理;各类丢番图方程的解法

　　进阶组合

　　随机过程和期望;复杂组合问题技巧、基本综合问题

　　AIME竞赛知识点

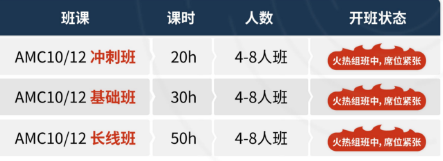
　　AMC数学竞赛培训   更多课程详情  咨询主页客服

　　思客教育总部位于深圳市福田区上梅林，拥有十年的国际竞赛辅导经验在北京、武汉、成都、杭州等城市开设了分部。对AMC竞赛培训有非常丰富的授课和培训经验，根据不同年级、不同数学基础的学生，推出了AMC课程：全程班100H，基础班50H、提高班30H、冲刺班20H。

　　思客教育AMC10/12获奖率72%，85%晋级AIME。AMC10及AIME培训课程，从历年真题入手，研发出独家教材，模块化学习，让孩子高效学习+有效练习(课后自习室)

　　班课人数：4-8人小班课/1V1定制化课程

　　授课时长：强化班-30课时;冲刺班-20课时;1V1定制化课时

　　课程亮点：独家讲义、1v1学管、课后自习室、同步提升校内数学